分析归并排序的时间复杂度，并证明

归并排序（Merge sort）

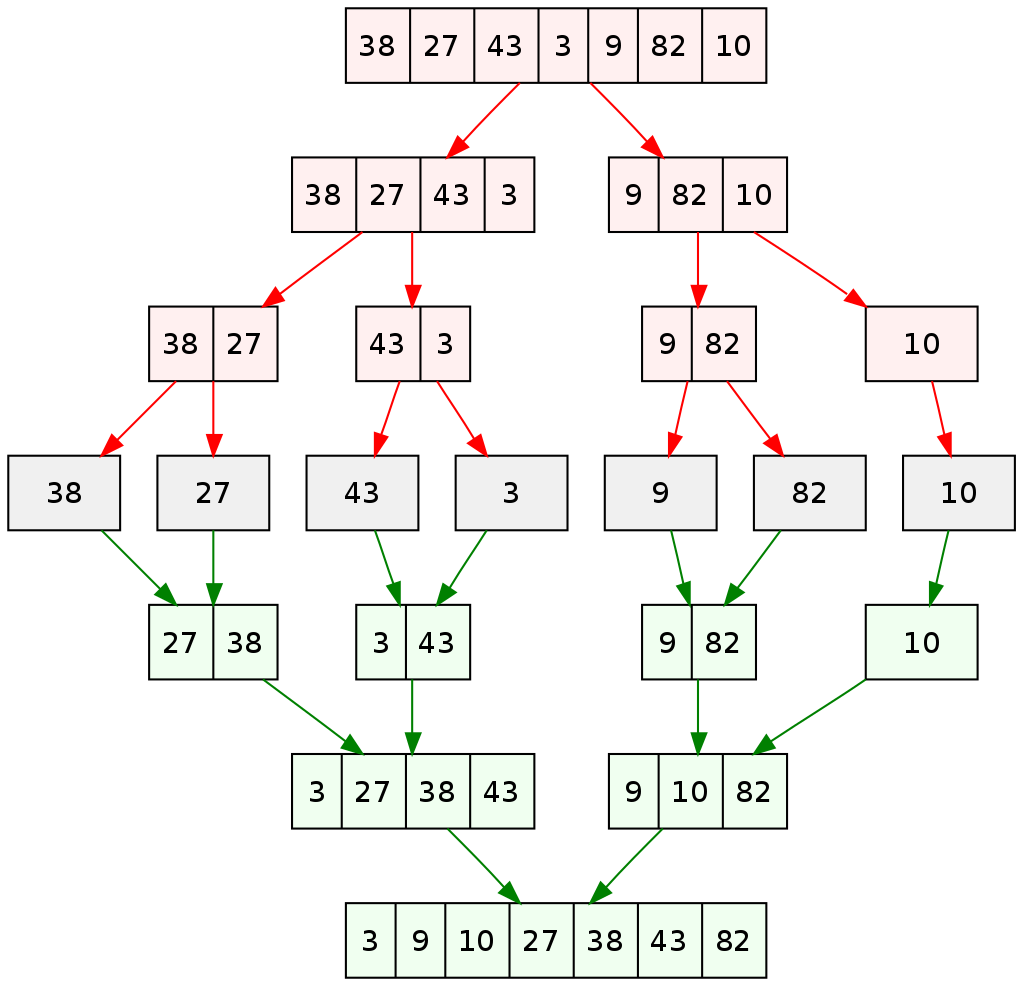
归并排序采用了分而治之的思想，过程可概括为以下几步：

• 将给定的待排序的数组一分为二
• 对两部分数组分别使用归并排序使其有序
• 将有序的两部分数组合并

MergeSort(arr[],l,r)
    if r > l
        middle m = (l+r)/2   //Find the middle point to divide the array into two halves
        mergeSort(arr,l,m)   //Call mergeSort for first half
        mergeSort(arr,m+1,r) //Call mergeSort for second half
        merge(arr,l,m,r)     //Merge the two halves sorted in step 2 and 3

复杂度证明（展开法）

根据算法的第一步可知

$T(N) =2 T(\frac{N}{2})+ O(N)$

• $T(n)$ 表示对$n$个数进行归并排序
• $2 T( n/2 )$表示将 $n$ 个数分成两部分分别进行归并排序
• $O(n)$ 表示对两个子过程结束之后合并的过程

$\begin{aligned} T(N) &=2 T(N / 2)+ O(N) \\ &=2\left(2 T(N / 4)+O(\frac{N}{2}) \right)+O(N) \\ &=4 T(N / 4)+ O(N)+2O(\frac{N}{2}) \\ &=4 T(N / 4)+2 O(N) \\ &=8 T(N / 8)+3 O(N) \\ & \vdots \\ &=2^{k} T\left(N / 2^{k}\right)+k O(N) \end{aligned}$

当 $N=2^{K}$ 时迭代停止，此时 $K=\log_{2}N$

代入，得

$T(N) = NT(1)+\log_2N\cdot{}O(N) = O(N\log{N})$

PS1: 这里假设 N 为偶数，如果不是，那么假设 N 介于 $2^i$ 和 $2^{i+1}$ 之间，通过估计 $T(2^{i+1})$ 来确定 $T(N)$ 的上界

PS2: $O(N) = aN=2O(\frac{N}{2})$，因为大O复杂度只看上界，所以其常数项可以被忽略， 来自于把一个待排序序列分解成两个序列的时间，这一操作可以在常数项内完成（设定一个下标的时间）。

复杂度证明（假设法）

假设 $T(N)=O(NlogN)\leq aN\log{N}+b$，$a,b$ 为常数。

$N=1$ 时，$T(1)=b$，成立

$N=k+1$ 时，$\frac{N}{2}=\frac{k+1}{2}\leq k$ 在 $N\geq 2$ 时成立

$T(\frac{N}{2})\leq a(\frac{N}{2})\log{\frac{N}{2}}+b$

因此，

$\begin{aligned} T(N)&\leq 2\textcolor{red}{T(\frac{N}{2})} + C_2N \quad//代入\\ &\leq 2（a(\frac{N}{2}\log{\frac{N}{2}}+b）+C_2N \\ &=aN\log{N}-aN\log2+C_2N+2b\\ &=aNlogN-aN+C_2N+2b \end{aligned}$

即

$T(N) \leq aNlogN-aN+C_2N+2b$

又因为假设 $T(N)=O(NlogN)\leq aN\log{N}+b$，使假设成立，则

$T(N) \leq \textcolor{red}{aNlogN-aN+C_2N+2b \leq aN\log{N}+b}$

解红线的式子，得

$-aN+C_2N+b \leq 0$

当 $a=C_1+C_2,\; b=C_1$ 时不等式成立。

得证