划分三角形问题

问能否将一个图完美的全部拆成一个个三角形，每个三角形的点互不重合。

实例： 图 G=(V,E),∣V∣=3q,qG=(V, E),|V|=3q, \quad q 为正整数。

询问： 是否存在 VV 的一个划分,将 VV 分成互不相交的 qq 个子集 V=V1∪V2∪⋯∪VqV=V_{1} \cup V_{2} \cup \cdots \cup V_{q} ， 使 ∣Vi∣=3\left|V_{i}\right|=3, 且 ViV_{i} 中的三个顶点形成三角形。

即设

Vi={vi[1],vi[2],vi[3]}V_{i}=\left\{v_{i[1]}, v_{i[2]}, v_{i[3]}\right\}

则

(vi[1],vi[2]),(vi[2],vi[3]),(vi[3],vi[1])∈E∘\left(v_{i[1]}, v_{i[2]}\right),\left(v_{i[2]}, v_{i[3]}\right) ,\left(v_{i[3]}, v_{i[1]}\right) \in E_{\circ}

该问题可以通过X3C问题归约证明。

NPC 证明

令 X3C 问题实例为布尔变量集合 S,∣S∣=3qS,|S|=3q 和项集合 C,ci={xi,yi,zi},∣C∣=nC,c_i=\{x_i,y_i,z_i\},|C|=n，以此构建划分三角形实例。

将项集合 CC 中的每一个元素替换为如下的子图（命名为三角子图）

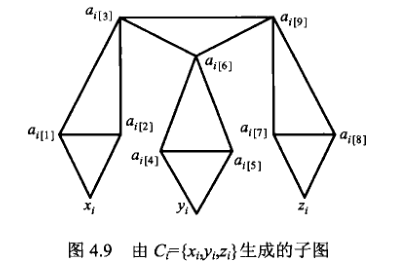
观察发现该图最多能划分出四个三角形（顶上一个，底下三个，注意划分出的三角形的点不能重复）。

而当去除任意 x,y,zx,y,z 中的一个或多个点后（和点相邻的边也被同时去除了），该图最多只能划分出三个三角形。

因此，所有的项可以按照这种替换方式，被完全替换成一个图结构。令每一个项 cic_i 替换成的子图表示为 Gi={Vi,Ei}G_i=\{V_i,E_i\}，则划分三角形实例的图结构表示为 G={V,E}G=\{V,E\}，其中：

E=⋃i=1nEi,(xi,yi,zi)=Ci∈C,∣Ei∣=18E=\bigcup_{i=1}^{n} E_{i},\left(x_{i}, y_{i}, z_{i}\right)=C_{i} \in C, |E_i|=18

易得∣E∣=18n|E|=18n

V=⋃i=1nViV=\bigcup_{i=1}^{n} V_{i}

注意每个子图的会额外在 X3C 布尔变量集合之外多定义 9 个点，即

Vi={xi,yi,zi}∪{ai[j]∣1≤j≤9}V_i=\{x_i,y_i,z_i\}\cup\{a_{i[j]}|1\leq j\leq 9\}

同样易得点个数 ∣V∣=∣S∣+9n=3q+9n|V|=|S|+9n=3q+9n

此时对于划分三角形实例，要求划分出的三角形个数 q′=q+3nq'=q+3n（点个数的 1/3）

(->) X3C 实例存在一个严格覆盖 C′C'，则对位于严格覆盖C′C'中的项，等价选择三角子图划分出四个三角形的情况；对于不在严格覆盖中的项，等价选择三角子图划分出三个三角形的情况。∣C∣=n|C|=n，因此一共是 n 个三角子图，∣C′∣=q|C'|=q 因此有 qq 个三角子图划分出 4 个三角形，n−qn-q 个三角子图划分出了 3 个三角形，一共是 4q+3(n−q)=q+3n4q+3(n-q)=q+3n 个三角形。

(<-) 假设图GG可以划分出 q+3nq+3n 个三角形。因为图 GG 中存在 nn 个三角子图（由项数决定），那么首先，肯定存在 qq 个三角子图划分出了 4 个三角形，其余的 n−qn-q 个三角子图划分出了 3 个三角形。

因为如果划分出4个三角形的三角子图数量不为 qq（假设是 q1q_1 个，那么最终的划分三角形个数即为 4q1+3(n−q1)=q1+3n≠q+3n4q_1+3(n-q_1)=q_1+3n \not= q+3n 。

那么对于这 qq 个三角子图GiG_i，对应选中 X3C 实例中的 Ci={xi,yi,zi}C_i=\{x_i,y_i,z_i\}，因为划分方式唯一，且划分三角形点没有重复，因此对应到 X3C 中就可以构成对 CC 的严格覆盖。

得证。