图的顶点覆盖问题（VC）

顶点覆盖是在一个图中找一些点集，这些点集能够覆盖所有的边。

最小顶点覆盖则要求点的数量是最小的。

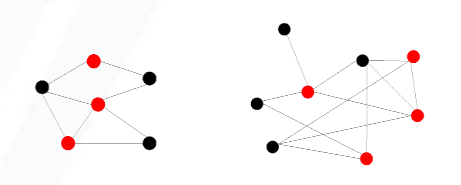
如下图，图中的两个图红色的点分别构成了这两个图的一个（最小）顶点覆盖，

顶点覆盖问题要求在一张图上找出不多于 K 个点的点集形成该图的一个顶点覆盖。其形式化定义为：

实例： 无向简单图 $G=(V, E),$ 一个非负整数 $K \leqslant \mid V_{\circ}$

询问： 图 $G$ 是否存在顶点覆盖 $V^{\prime} \subseteq V$ 且 $\mid V' \leqslant K_{\circ}$ 所谓顶点覆盖 $V^{\prime}$ 是指 $G$ 中任意边 $(u, v) \in E$ 至少有一个顶点属于 $V^{\prime}, \quad$ 即 $\{u, v\} \cap V^{\prime} \neq \varnothing_{\circ}$

该问题通过将 3SAT 归约到 VC 来完成。

核心思路

以 3SAT 实例 $U=\left\{u_{1}, u_{2}, u_{3}, u_{4}\right\}$ 及 $C=\left\{\left\{u_{1}, \bar{u}_{3}, \bar{u}_{4}\right\},\left\{\bar{u}_{1}, u_{2}, \bar{u}_{4}\right\}\right\}$ 为例，构建出的顶点覆盖实例如下所示：

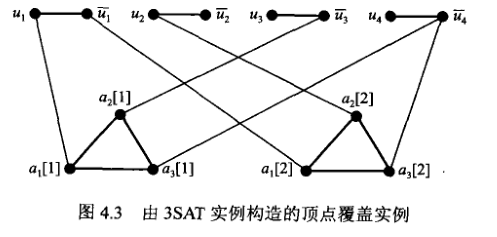
该实例由三部分组成：每一个布尔变量的正反项生成两个顶点和一条边（表示为一条直线（命名为线集），每一个项生成三个顶点和三条边（表示为一个三角形）（命名为三角形集）。最后，每个线图和每个三角形图之间通过项的组成再次连接直线（命名为边集）。注意每个三角形的每个点各自和边集中的一条边对应。

(->）当 3SAT 实例存在真值指派时，遍历一遍 $U$ 中每个布尔变量 $u_i$的真值指派，如果 $u_i=T$，那么在顶点覆盖中就选择 $u_i$，否则就选择 $\bar{u_i}$，这种方式保证了所有的线集都被覆盖。此时，每个三角形对应的边集中的三条边中至少有一条边也被覆盖（被线集中的一个点覆盖，这对应着每个三角形对应的项的析取值均为 $T$）。之后如果要完成顶点覆盖，还需要从三角形中选择点来覆盖剩余的边集和三角形集。

对边集的覆盖，只需要在每个三角形中选择最多两个点（最少不用选，此时三角形对应的边集中的三条边都已经被相应线集中的点覆盖），即可覆盖全部还未选中的边集。

最后遍历每个三角形，对之前在每个三角形中选择少于两点的情况，任意选取点，补全两点的情况（三角形只需要两点即可选中），即可覆盖全部三角形集。

(<-) 当实例存在顶点覆盖集 $V'$ 时，可得 $V'$ 一定会包含每个线图的一个顶点，以及每个三角形的两个顶点（反证法，如果每个线图都没有顶点的话，那么没有其他的点可以用于覆盖两点之间的线，三角形同理）。

因此还剩下最后边集的覆盖。由于每一个三角形上的两个顶点都能覆盖边集上的两条边，因此还需要来自于顶部线图中的点覆盖第三条边，这样就形成了一个对应关系：每一个三角形实际上对应的是3SAT中的一个项，选择一个点来覆盖第三条边实际上就是让相应的布尔变量指派为真。因此，让顶点覆盖中来自于线图的点对应的布尔变量的指派为真，即可得到解决 3SAT 问题的真值指派。