P(polynominal, 多项式)

即在多项式时间内可解的问题

NP(Nondeterministic polynominal, 非确定性多项式)

存在一部分问题，没有办法在多项式时间内解决，但能在多项式时间内验证某一答案是否正确。

如果有一台非确定型图灵机，那么一个 NP 问题就可以在穷举所有答案后在多项式时间内被解答出来（理想情况下，所有答案在同一时间被穷举，然后在剩下的多项式时间内被同时验证）。

随后就有一个很著名的问题，即 NP类问题等于 P类问题吗？是否所有能在多项式时间内验证得出正确解的问题，都是具有多项式时间算法的问题呢？

一旦解决这一问题，那么所有的 NP 问题都可以通过计算机来解决。

解决这一问题的一个办法，就是归约法。如果问题B的算法可以用来解决A（不要求 A 的算法能解 B），我们就说问题A可以归约成问题B。比如二元一次方程和一元一次方程的求解方法。显然二元一次方程的解法可以用来求解一元一次方程（令二次项系数为0）。

因为归约是具有传递性的，即如果 A 可以归约到 B，B 可以归约到 C，A 就可以归约到C。

那么如果有一个终极的 NP 问题，其他所有的 NP 问题都可以归约到这个问题上，那么当这一个终极 NP 问题解决时，所有的 NP 问题就都解决了。

如果这个终极的问题存在，那么这个终极问题就被称为是 NPC，能归约到该问题上的其他问题被称为NPC类问题。

现在，只剩下一个问题了，就是是否存在 NPC 类问题？

1970年 Cook 证明了第一个 NPC 问题。

存在一些 NPC 问题，当问题中的某个数值参数固定或存在上限时，该问题可以被一个多项式时间算法验证，这类问题在 NPC 问题中相对更加简单，解决的多项式时间算法叫伪（pseudo）多项式时间算法。

而在 NPC 类问题中，除去上面描述的存在伪多项式时间算法的 NPC 类问题后，剩下问题就属于强 NPC 类问题。强 NPC 类问题一定不存在伪多项式时间算法。

一个例子是划分问题的动态规划算法，可以参考书中 P124 了解。

NP困难（NP-hard）难在不一定在多项式时间内被验证正确性，即使NP完全问题有多项式时间的解（P=NP），NP困难问题依然可能没有多项式时间的解。因此NP困难问题 “至少与NP完全问题一样难” 。

因此， NPC 问题也可以看做是 NP-hard，其属于 NP-hard 的子集。

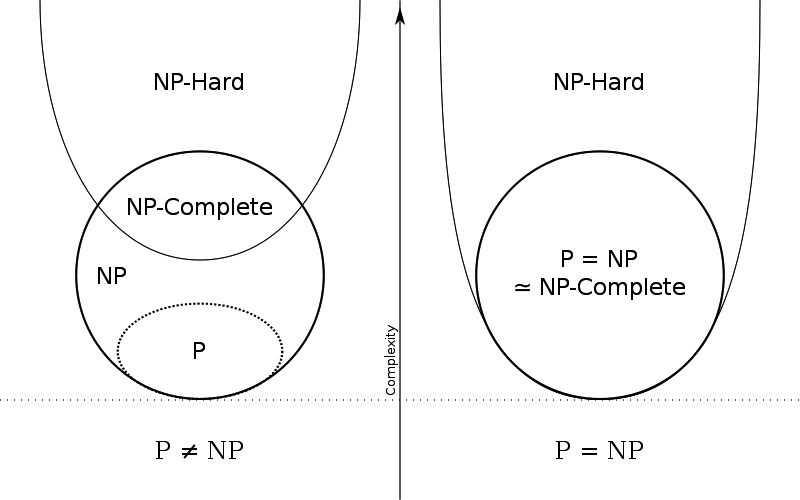
当 $P\not=NP$ 时，NP问题和 NP-hard 的交集就是 NPC 问题；当 $P=NP$ 时， $P=NP=NPC$ ，如下图所示：

NP-hard 问题由图灵归约得到，有三种途径：

一个问题能由任意一个NP问题图灵归约到该问题，则该问题是NP-Hard。
一个问题能由某个NPC问题图灵归约到该问题，则该问题为NP-hard。
若 $\pi_{1}$ 是NP-hard问题， $\pi_{1}$ 可以图灵归约到 $\pi_{2}$ （即 $\pi_{1}\propto_t \pi_{2}$ ）, 则 $\pi_{2}$ 也是NP-hard问题。